Sin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved example Introduction to Tan double angle formula2319Proving the trigonometric identity $(\tan{^2x}1)(\cos{^2(x)}1)=\tan{^2x}$ has been quite the challenge I have so far attempted using simply the basic trigonometric identities based on the Pythagorean Theorem I am unsure if these basic identities are unsuitable for the situation or if I am not looking at the right angle to tackle this problemVerify the Identity tan(2x)^2sin(2x)^2cos(2x)^2=sec(2x)^2 Start on the left side Apply Pythagorean identity Tap for more steps Apply pythagorean identity Apply pythagorean identity Because the two sides have been shown to be equivalent, the equation is an identity is an identity

1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube
Tan 2x identity proof
Tan 2x identity proof-Identities related to sin 2x, cos2x, tan 2x, sin3x, cos3x, and tan3x Sin 2x = Sin 2x = sin(2x)=2sin(x) cos(x) Sin(2x) = 2 * sin(x)cos(x) Proof To express Sine, the formula of "Angle Addition" can be usedTanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac {\cos ^2 x} {1\tan x}
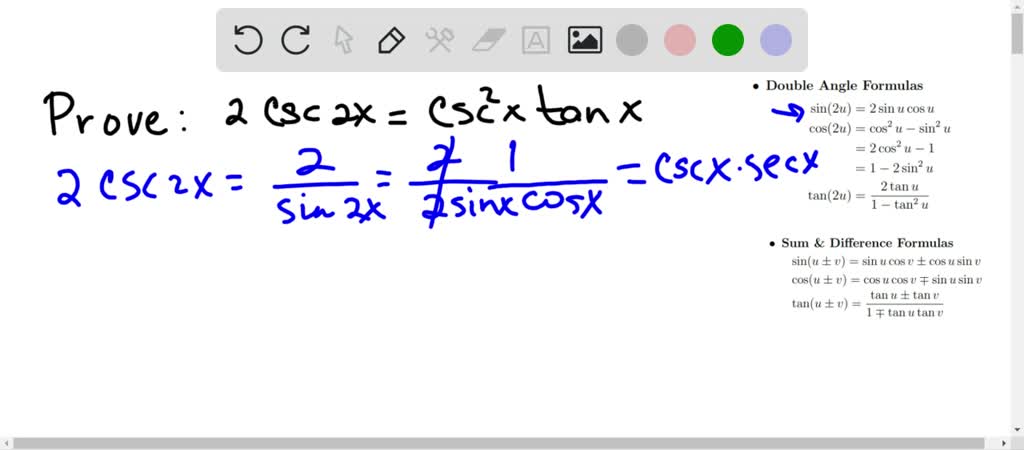


Solved In Exercises 15 22 Prove The Identity 2
Sum and Difference Identities For the exercises 14, find the exact value 1) \(\tan \left (\dfrac{7\pi }{12} \right )\) Answer \(2\sqrt{3}\)In this video, we are going to derive the identity for the tangent of 2xThe identity for tan(x y) has been explained in the following videohttps//youtubYes, sec2 − 1 = tan2x is an identity
Free trigonometric identity calculator verify trigonometric identities stepbystep This website uses cookies to ensure you get the best experience ByVerify the identity 1 cos 2x tan x = sin 2x Use the appropriate doubleangle formulas to rewrite the numerator and dena simplified 1 cos 2x sin 2x 1 Simplify the numerator Enter denominator found in the previ The expression from the previous step then simplifies to tan x using what?Trigonometric Identities and Formulas Below are some of the most important definitions, identities and formulas in trigonometry Trigonometric Functions of Acute Angles sin X = opp / hyp = a / c , csc X = hyp / opp = c / a tan X = opp / adj = a / b , cot X = adj / opp = b / a cos X = adj / hyp = b / c , sec X = hyp / adj = c / b ,
Proving Trigonometric Identities Calculator online with solution and steps Detailed step by step solutions to your Proving Trigonometric Identities problems online with our math solver and calculator Solved exercises of Proving Trigonometric IdentitiesThe double‐angle identity for tangent is obtained by using the sum identity for tangent The half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 Verify the identityThese identities are sometimes known as powerreducing identities and they may be derived from the doubleangle identity \(\cos(2x)=\cos^2x−\sin^2x\) and the Pythagorean identity \(\cos^2x\sin^2x=1\)



How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic



Trig Identities Bingo Card
2 x I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way ever Not sure why I can't do that, but something was wrong Anyways I looked at the solutions manual and they magic out 1 tan x tan 2 x = 1 tanThe more important identities You don't have to know all the identities off the top of your head But these you should Defining relations for tangent, cotangent, secant, and cosecant in terms of sine and cosine The Pythagorean formula for sines and cosines This is probably the most important trig identityCos 2x ≠ 2 cos x;



Answered Verify The Identity 2 Tan X 1 Bartleby



How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
I need to prove this identity tan^2xsin^2x = tan^2xsin^2x start with left side tan^2xsin^2x =(sin^2x/cos^2x)sin^2xIdentity tan (2x) Multiple Angle Identities Symbolab Identities Pythagorean Angle Sum/Difference Double Angle Multiple Angle Negative Angle Sum to Product Product to SumThese identities can be useful in calculus for converting rational functions in sine and cosine to functions of t in order to find their antiderivatives Technically, the existence of the tangent halfangle formulae stems from the fact that the circle is an algebraic curve of genus 0


Prove Tan 2x Cos 2x Cot 2x Sin 2x 1



Weierstrass Substitution Wikipedia
• Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;X) 2 1 = 1 cos 2 x There aren't any terms or factors involving in this formula, so let's make up another one An equivalent formula for is math\implies\tan^2x=\dfrac {\sin^2x\sin^2x\cos^2x} {\sin /math Continue Reading2617I'm currently stumped on proving the trig identity below $\tan(2x)\tan (x)=\frac{\tan (x)}{\cos(2x)}$ Or, alternatively written as $\tan(2x)\tan (x)=\tan (x)\sec



Trig Double Identities Trigonometric Double Angle Functions Trig



How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic
Tan 2x ≠ 2 tan x by Shavana GonzalezIn this video you will learn how to verify trigonometric identitiesverifying trigonometric identitieshow to verify trig identitieshow to verify trigonometricExcellent application of Pythagorean Trig Identities email anilanilkhandelwal@gmailcom



1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube


Ilectureonline
Math2org Math Tables Trigonometric Identities sin (theta) = a / c csc (theta) = 1 / sin (theta) = c / a cos (theta) = b / c sec (theta) = 1 / cos (theta) = c / b tan (theta) = sin (theta) / cos (theta) = a / b cot (theta) = 1/ tan (theta) = b / a sin (x) = sin (x)Explanation Change to sines and cosines then simplify 1 tan2x = 1 sin2x cos2x = cos2x sin2x cos2x but cos2x sin2x = 1 we have ∴ 1 tan2x = 1 cos2x = sec2x Answer linkThe inverse trigonometric identities or functions are additionally known as arcus functions or identities Fundamentally, they are the trig reciprocal identities of following trigonometric functions Sin Cos Tan These trig identities are utilized in circumstances when the area of the domain area should be limited These trigonometry functions have extraordinary noteworthiness



Weierstrass Substitution Wikipedia
.JPG)


Every Day I M Calculatin I D3 Unit Q Pythagorean Identities
Trigonometric Identities Sum and Di erence Formulas sin(x y) = sinxcosy cosxsiny sin(x y) = sinxcosy cosxsiny cos(x y) = cosxcosy sinxsiny cos(x y) = cosxcosy sinxsiny tan(x y) = tanxtany 1 tanxtany tan(x y) = tanx tany 1tanxtany HalfAngle Formulas sin 2 = q 1 cos 2 cos 2 = q 1cos 2 tan 2 = q 1cos tan 2 = 1 cosx sinx tan 2 = sin 1cos1610How to prove the trigonometry equation is an identity?Therefore in mathematics as well as in physics, such formulae are useful for deriving many important identities The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is



Integrate Tan 2x


How To Find Sin2x Cos2x And Tan2x If Tanx 3 4 And X Terminates Quadrant I Quora
Question I need to prove this identity tan^2xsin^2x = tan^2xsin^2x Answer by lwsshak3() (Show Source) You can put this solution on YOUR website!Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4 cot x = 1/tan x equation 5 sin 2 x cos 2 x = 1 equation 6 tan 2 x 1 = sec 2 x equation 7 1 cot 2 x = csc 2 x equation 8 cos (x y) = cos x cos y sin x sin y equation 9 sin (x y) = sin x cos y cos x sin y equation 10 cos (x) = cos x equation 11O A Pythagorean Identity OB Quotient Identity OC


Prove The Identity Secxcscx Tanx Cotx 2 Tan 2x Cot 2x1 Apply The Distributive Property2 Apply The Brainly Com



7 Techniques Of Integration Techniques Of Integration 7
Verify the Identity (1sin(x)^2)(1tan(x)^2)=1 Start on the left side Apply Pythagorean identity Tap for more steps Apply pythagorean identity Rearrange terms Apply pythagorean identity Convert to sines and cosines Tap for more steps Apply the reciprocal identity to Apply the product rule toThe denominator 1 tan^2(x) = = = (2) 3 When you divide the numerator (expression (1)) by the denominator (expression (2)), cos^2(x) cancels, and the remaining expression isSafety How works Test new features Press Copyright Contact us Creators


7 Proving Ids Trig Functions Identities



Topic Lesson Trigonometric Functions
$\cos{2\theta}$ $\,=\,$ $\dfrac{1\tan^2{\theta}}{1\tan^2{\theta}}$ A mathematical identity that expresses the expansion of cosine of double angle in terms of tan squared of angle is called the cosine of double angle identity in tangent Introduction LetAs there is no way to immediately integrate tan^2(x) using well known trigonometric integrals and derivatives, it seems like a good idea would be writing tan^2(x) as sec^2(x) 1 Now, we can recognise sec^2(x) as the derivative of tan(x) (you can prove this using the quotient rule and the identity sin^2(x) cos^2(x) = 1), while we get x when we integrate 1, so our final answer is tan(x)Trigonometric Identities ( Math Trig Identities) sin (theta) = a / c csc (theta) = 1 / sin (theta) = c / a cos (theta) = b / c sec (theta) = 1 / cos (theta) = c / b tan (theta) = sin (theta) / cos (theta) = a / b cot (theta) = 1/ tan (theta) = b / a sin (x) = sin (x)



Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco



Ch Ppt Download
In mathematics, an identity is an equation which is always true These can be trivially true, like x = x or usefully true, such as the Pythagorean Theorem's a2 b2 = c2 for right triangles There are loads of trigonometric identities, but the following are$$2\cot4x = \cot2x \tan2x$$ Thank you in advance Thank you for the comments and hints I got an answer after many tries ;) Below is my answer Thank you $2cot4x = cot2x tan2x$ $2\frac{1}{tan 4x} = cot2x tan2x$ $2\frac{1}{\frac{2 tan 2x}{1 tan^2 2x}} = cot2x tan2x$Deriving the derivative of $\tan^{2}x$ by quotient rule using $$\frac{\sin x}{\cos x}$$ identity, i am getting a different value $2\sec x\tan x\tan^{2}x$ than


Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities



1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &We rearrange the trig identity for sin 2 2x We divide throughout by cos 2 2x The LHS becomes tan 2 2x, which is our integration problem, and can be expressed in a different form shown on the RHS However, we still need to make some changes to the first term on the RHS We recall a standard trig identity with secx This is usually found in formula booksAnswered 2 years ago tan (x) is an odd function which is symmetric about its origin tan (2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin (2x) to cos (2x) sin (2x) = 2 sin (x) cos (x)



Solved In Exercises 15 22 Prove The Identity 2
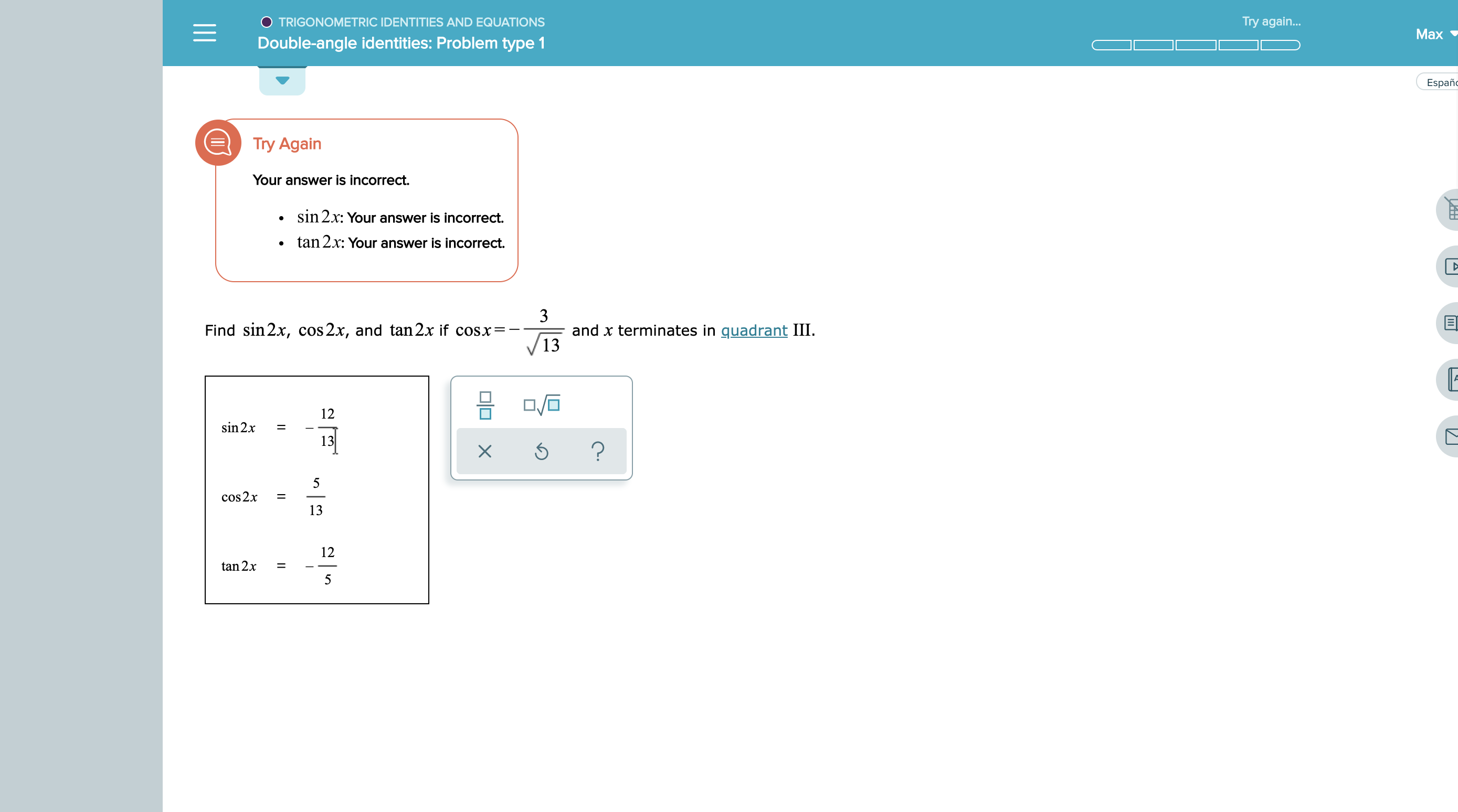


Answered Try Again Trigonometric Identities Bartleby
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengths They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
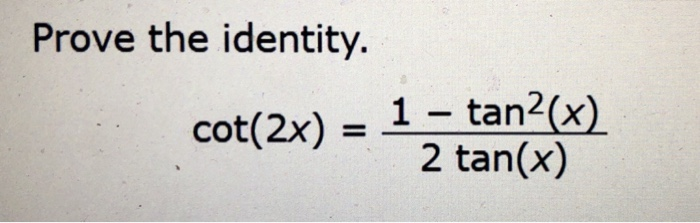


Solved Prove The Identity Cot 2x 1 Tan2 X 2 Tan X Chegg Com



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2



Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube



The General Solution Of The Equation Tanx Tan 2x Tan 2x Tanx 2 0


Prove The Identity Tan P 4 X Tan P 4 X 2 Sec 2x Sarthaks Econnect Largest Online Education Community



Lw00plbaiwnh4m


Sin 2x Cos 2x And Tan 2x



Which Of The Following Expressions Completes The Identity 1 Sec 2 X Mathematics Stack Exchange



Integration Of Trigonometric Functions



Integrate Tan 2x By Parts



Trig Identities Bingo Card



Tan2x ただの悪魔の画像


Trig Identities Hsn Forum



Solved Verify The Identity 4 2 Tan X Secx2tan X 1 Whic Chegg Com



Int 4sec 2xtanx Sec 2x Tan 2x Dx Log 1 F X C


Prove The Identity Cos 2x 1 Sin 2x Tan P 4 X Sarthaks Econnect Largest Online Education Community



Solve Tan 2 X 1 0 Yahoo Answers Noha Matthieu Lire Un Livre
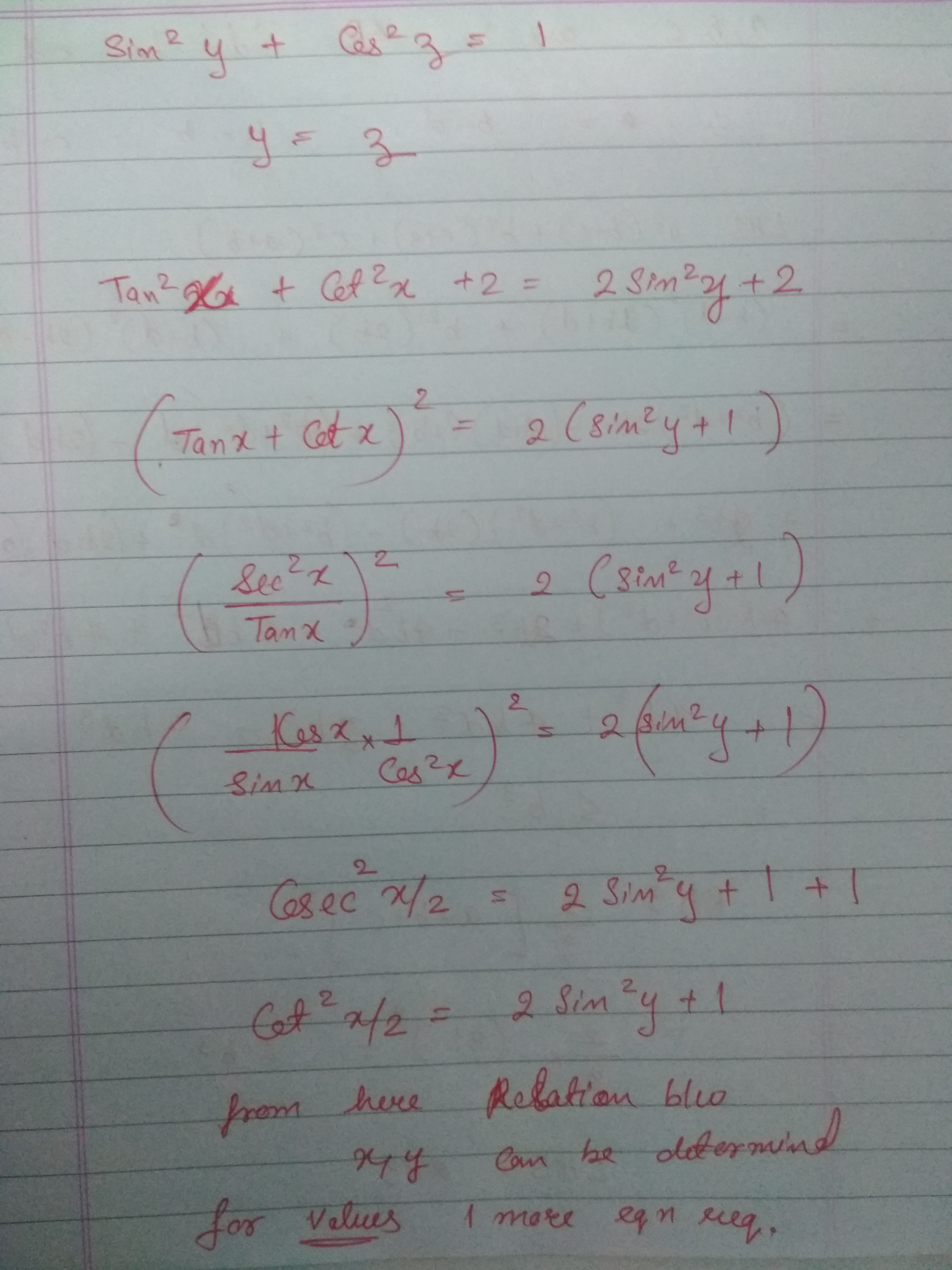


Solve For X Y And Z If Tan 2x Cot 2x 2sin 2y And Sin 2y Cos 2z 1 Askiitians



Tangent Half Angle Formula Wikipedia


A Trig Identity



Solved 5 2 Verify The Following Trigonometric Identities Chegg Com



Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com
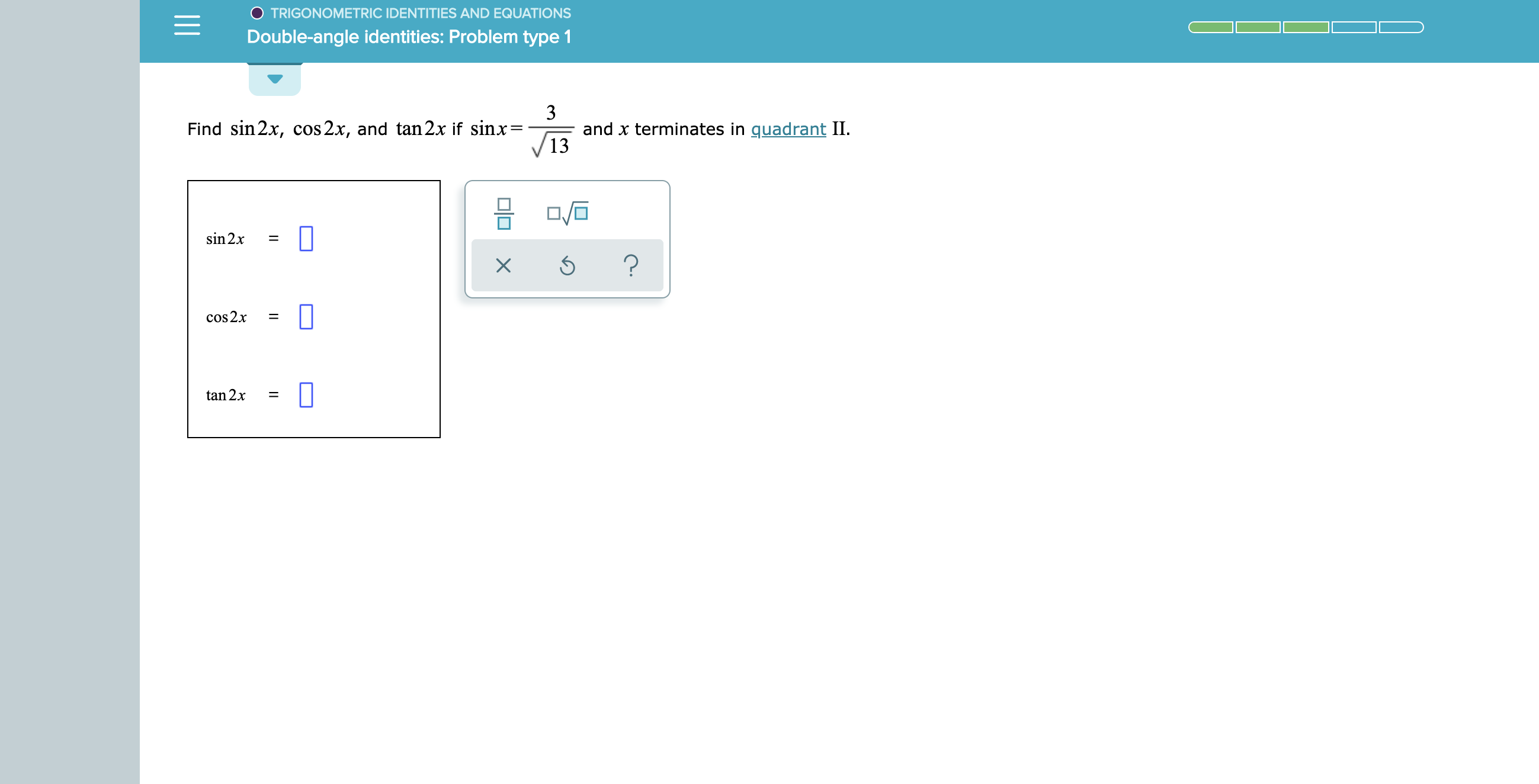


Answered Trigonometric Identities And Equations Bartleby



Tan 2x Identity Learn Lif Co Id
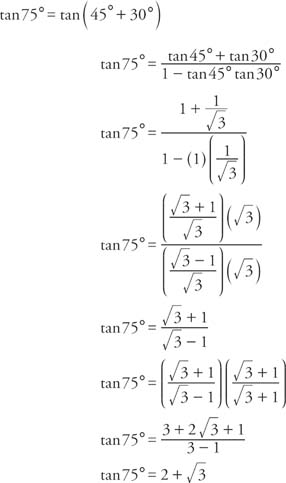


Tangent Identities



Integrate Sec 2x Method 2



How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic



Trig Identity Sec2x Minus Tan2x T10 Youtube



How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube



Scrollingdiv Withhtml Mytutorial



Sum And Difference Identities Video Lessons Examples And Solutions


Trig Identities Hsn Forum



Solved Verify That The Equation Is An Identity Tan 2x Chegg Com



Double Angle Trig Identities Quiz Quiz Quizizz


Solution Show All Steps Necessary To Verify The Trigonometric Identity 1 Tan 2x Csc 2x Tan 2x



9 1 Identities And Proofs Ppt Download
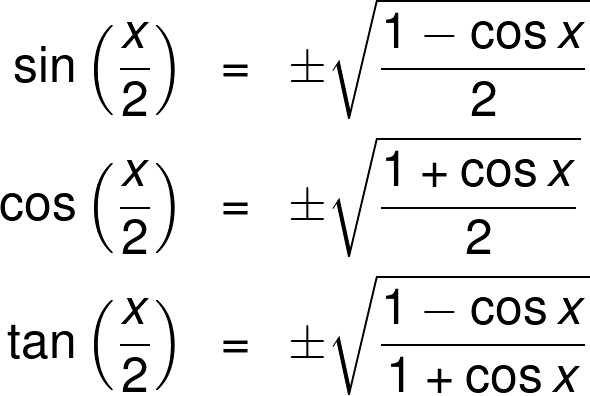


Half Angle Calculator



Double Angle And Half Angle Identities Example Sin 28 Cos 2a Or Tan 2x
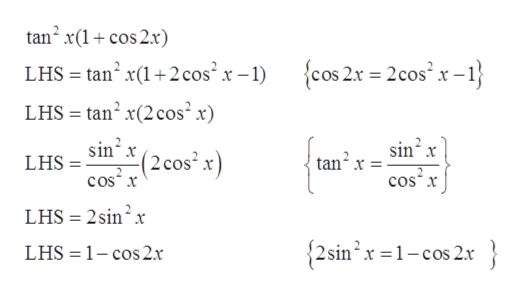


Answered Tan2x 1 Cos2x 1 Cos2x Verify The Bartleby



Tangent Half Angle Formula Wikipedia



Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Trigonometry Precalculus Math



Chapter 11 Trigonometric Identities And Equations 11 1


Biomath Trigonometric Functions



Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity



Consider The Following Equations 1 Cosec 2x Sec 2x Cosec 2xsec 2x 2 Sec 2x Tan 2x Sec 2xtan 2x 3 Cosec 2x Tan 2x Cot 2x



Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction


Prove That Cos2x Cos 2x Sin 2x 2cos 2x 1 1 2sin 2x 1 Tan 2x 1 Tan 2x Sarthaks Econnect Largest Online Education Community



Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube


Simplify The Trigonometric Expression Tan 2x Tan X Using Double Angle Identities A Brainly Com


Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero



Tan2x Tanx Tanx Sec2x Maths Trigonometric Functions Meritnation Com



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic


How To Prove Csc 2x 1 Tan 2x 1 Is Equivalent To Cosec 2x Quora



Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x



Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi



Integrate Sec 2x Method 1


Trig Identity Question



Trigonometric Identities Aqa A Level Maths Pure Revision Notes


True Or False The Equation Sec 2 X 1 Tan 2 X Is An Identity Brainly Com



Packet 21 Trigonometric Identities Ppt Download



Solved Prove The Identity 4 Tan 3x 12 Tan X 4 Tan 3 Chegg Com
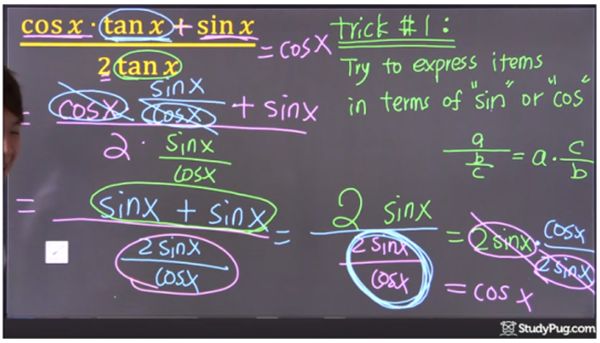


How To Prove Quotient And Reciprocal Identities Studypug
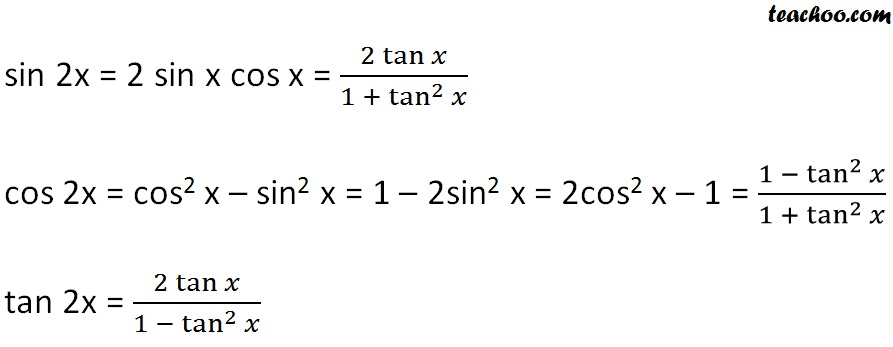


Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi



How To Use Trig Identities Mathematics Stack Exchange


What Is The Formula Of Tan2x Quora


What Is The Formula Of Tan2x Quora



14 2 Trigonometric Identities



Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube



Analytic Trig Ppt Video Online Download


Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities



Trig Identities And Formulas Pre Calculus Quiz Quizizz
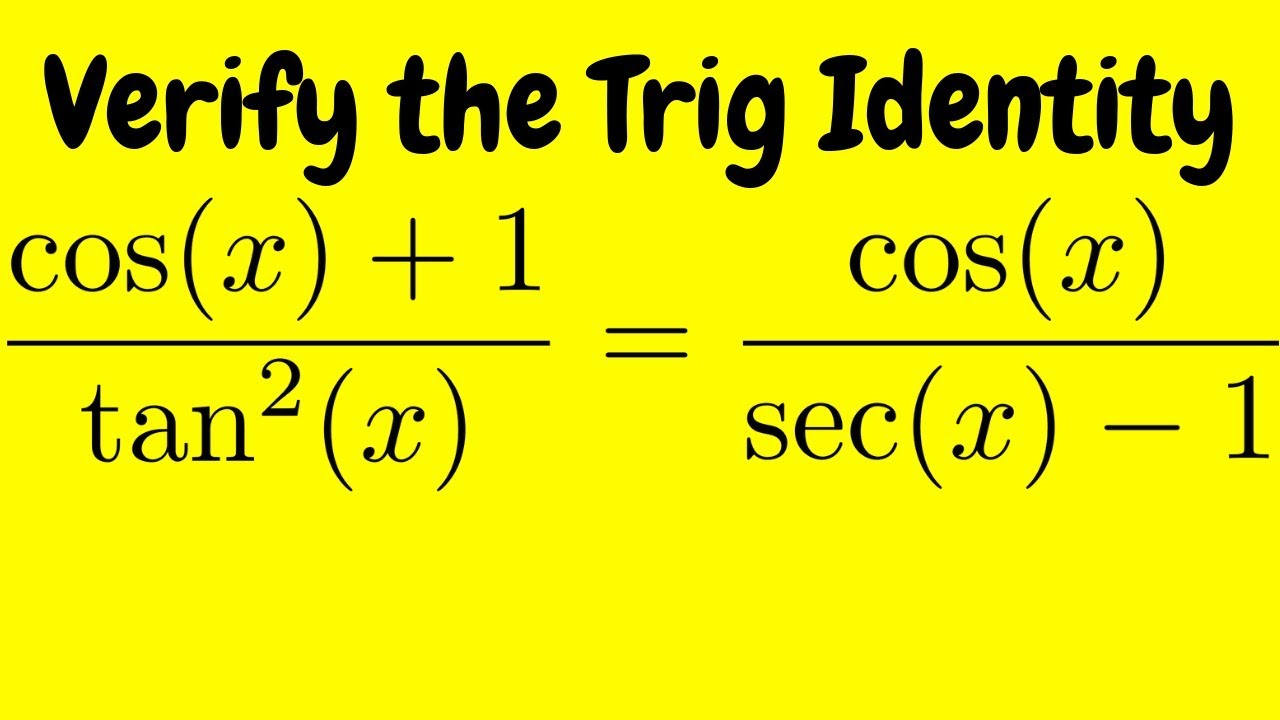


Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube


What Is The Formula Of Tan2x Quora



7 2 47 Integral Of 1 Tan2x Sec2x Cute766
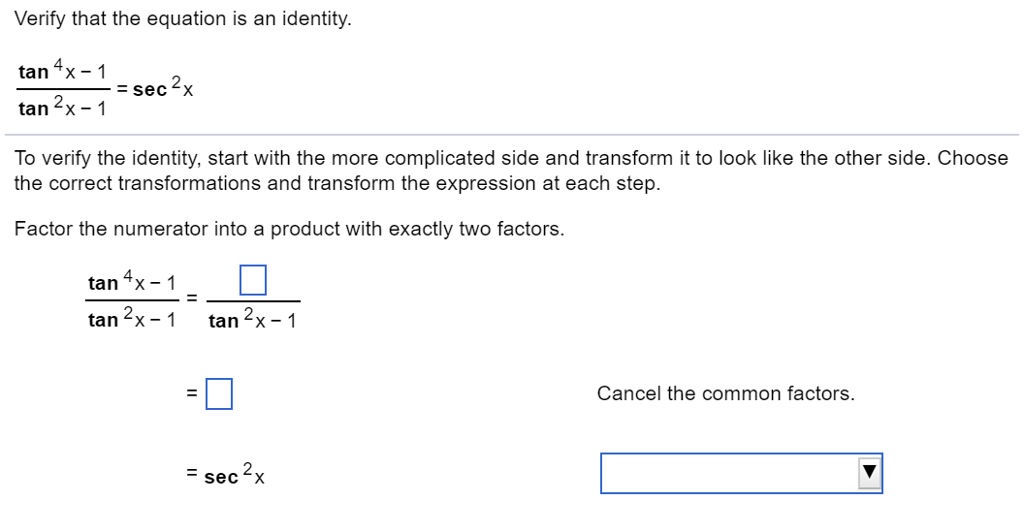


Solved Verify That The Equation Is An Identity Tan 4x 1 Chegg Com



0 件のコメント:
コメントを投稿