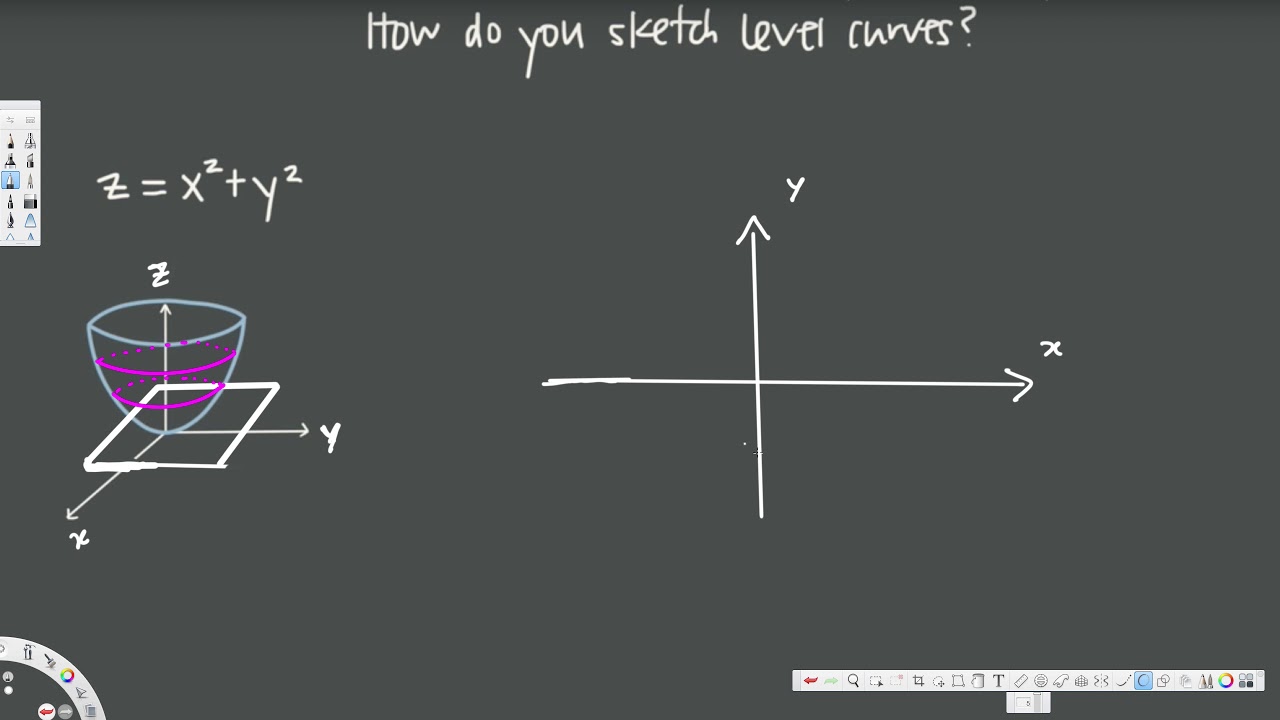
Level Curves So far we have two methods for visualizing functions arrow diagrams and graphs A third method, borrowed from mapmakers, is a contour map on which points of constant elevation are joined to form contour curves, or level curves A level curve f (x, y) = k is the set of all points in the domain of f at which f takes on a given value kIn mathematics, a level set of a realvalued function f of n real variables is a set where the function takes on a given constant value c, that is L c = { ∣ f = c }, {\displaystyle L_{c}=\left\{\mid f=c\right\}~,} When the number of independent variables is two, a level set is called a level curve, also known as contour line or isoline;Download Wolfram Player Let be a realvalued function of two real variables and let be a constant The set of all points (, ) in the plane such that is called a level curve of (with value ) Contributed by Osman Tuna Gökgöz (March 11)

Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id
Level curves of a function f
Level curves of a function f-Describe the level curves of the function z = 6 − 2x − 3y Sketch a contour map of the surface using level curves for the given cvalues c = 0, 2, 4, 6, 8, 10Sketch a contour map of the surface using level curves for the given cvalues 6 6 5 CES 4 3 C = 2 1 1 X 13;




The Field Of The Condenser And The Level Curves Of The Function U For Download Scientific Diagram
Describe the level curves of the function Sketch a contour map of the surface using level curves for the given cvalues z= xy, c=1, 0, 2, 4 Explanation A Explanation B The 3 − D 3D 3 − D graph of function z = x y z=xy z = x y Is a plane and contour of curve are line with respective value ofDescribe the level curves of the function Sketch the level curves for the given c values f(x, y)=\frac{x}{x^{2}y^{2}}, \quad c=\pm \frac{1}{2}, \pm 1, \pm Boost your resume with certification as an expert in up to 15 unique STEM subjects this summerDefinition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f ) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f
Remark 1 Level curves of a function of two variables can be drawn in an ( x, y) coordinate system; Returning to the function \(g(x,y)=\sqrt{9−x^2−y^2}\), we can determine the level curves of this function The range of \(g\) is the closed interval \(0,3\) First, we choose any number in this closed interval—say, \(c=2\) The level curve corresponding to \(c=2\) is described by the equation \ \sqrt{9−x^2−y^2}=2\ The left side is your z = y2 2y x2 − 2x and the two constants on the right are the two values of z that are your level curves
A level curve of a function of two variables is completely analogous to a contour line on a topographical map (a) A topographical map of Devil's Tower, Wyoming Lines that are close together indicate very steep terrain (b) A perspective photo of The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equations of the level curves are \(f\left( {x,y} \right) = k\) Note that sometimes the equation will be in the form \(f\left( {x,y,z} \right) = 0\) and in these cases the equations of the level curves are \(f\left( {x,y,k} \right) = 0\)C Graph the level curve AHe, iL=3, and describe the relationship between e and i in this case T 37 Electric potential function The electric potential function for two positive charges, one at H0, 1L with twice the strength as the charge at H0, 1L, is given by fHx, yL= 2 x2 Hy1L2 1 x2 Hy 1L2 a Graph the electric potential using the window @5, 5Dµ@5, 5Dµ@0, 10 D



Solved The Figure Shows Level Curves Of A Functio




Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube
Level Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the corresponding curves on the surface, the 1624 // Summary for how to sketch level curves Whenever you're dealing with a multivariable function, the graph of that function will be a threedimensional figure in space If you take a perfectly horizontal sheet or plane that's parallel to the xyplane, and you use that to slice through your threedimensional figure, then what you get at the intersection of the figure and the plane is a twodimensional curveGraph several level curves of the following function using the given window Label at least two level curves with their Zvalues Z= = 132 – x2 y2166*6,6 Choose the correct graph below A B D E OF OG Ο Η Question Graph several level curves of the following function using the given window Label at least two level curves




Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download



Answered Sketch The Level Curves Of The Function Bartleby
For example, level curves of the range function defined by \(f(x, y) =\dfrac{x^2 \sin(2y)}{32}\) plotted in the xyplane are shown in Figure 910 If we lift these contours and plot them at their respective heights, then we get a picture of the surface itself, as illustrated in Figure 911 Figure 910 Several level curves Figure 911 LevelThe level curves are The graph of a two variable function in 3D A set of curves tangent to the gradient of a function O A set of plane curves that describe aHow to Find the Level Curves of a Function Calculus 3 How to Find the Level Curves of a Function Calculus 3



Gradients Level Curves




Oneclass Find The Domain And Range And Describe The Level Curves For The Function F X Y F X Y V4
Describe the level curves of the function Sketch the level curves for the given c values z = 6 − 2 x − 3 y, c = 0, 2, 4, 6, 8, 10Level Curves In mathematics, a level set of a realvalued function f of n real variables is a set where the function takes on a given constant value c Plotting 3d graphs and level curves in Matlab I have the following code below, but I cannot test it since I do not have Matlab with me right now and I am afraid I might not have the time to test it by myself when I finally get it I'm trying to plot both 3d graphs and graphs of the level curves in the y and x axis (two dimensions only) of




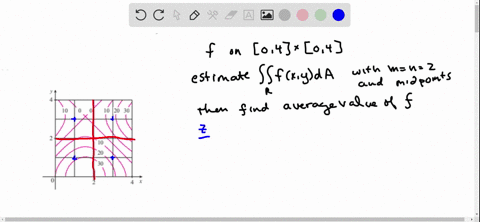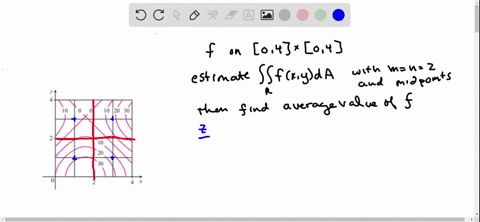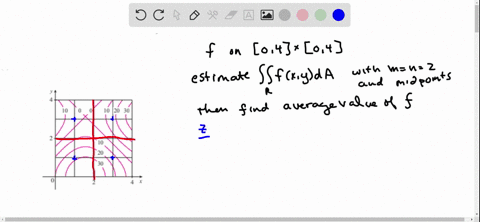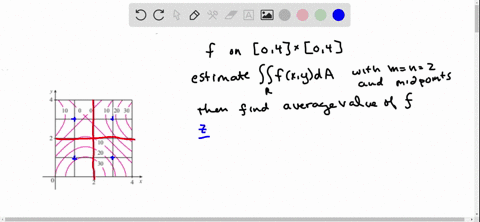
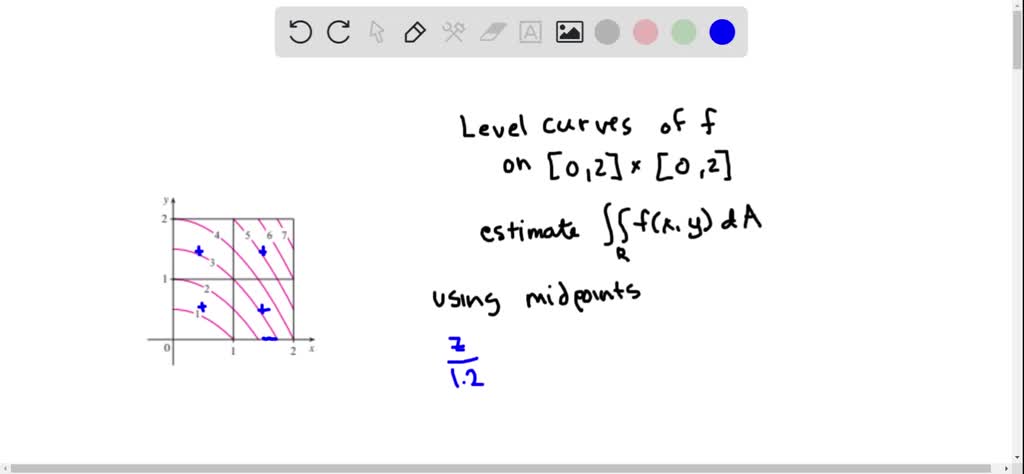
The Figure Shows Level Curves Of A Function F In The Square R 0 6 Times 0 6 Use The Midpoint Rule With M N 2 To Estimate



Contour Lines Rodolphe Vaillant S Homepage
Question Describe the level curves of the function z = x y C = 2, 2, 3,5 O The level curves are circles O The level curves are parallel lines The level curves are noncircular ellipses The level curves are hyperbolasThere is a close relationship between level curves (also called contour curves or isolines) and the gradient vectors of a curve Indeed, the two are everywhere perpendicular This handout is going to explore the relationship between isolines and gradients to help us understand the shape of functions in three dimensions This is a common application in physics when considering lines of2279 Now if someone gives you a quadratic equation of this type– that is, an equation involving two variables, x and y– and you see that there are terms with x squared, y squared, also x y in general is a quadratic term, and then some linear terms, d x and e y in a constant and ask you to find the level curve of that quadratic function of



Solved Define The Level Curves Of A Function Of Two Variables Give Examples Of Several Surfaces Whose Level Curves Are Circles And At Least One Ex Course Hero




Presentation On Introduction To Several Variables And Partial Derivat
Definition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f has height kSo a level curve is the set of all realvalued solutions of anFrom the definition of a level curve above, we see that a level curve is simply a curve of intersection between any plane parallel to the $xy$ axis and the surface generated by the function $z = f (x, y)$ For example, consider the two variable realvalued function $f




Two Level Curves Of A Function V X Y In A Two Dimensional 2d Download Scientific Diagram



Level Curves And The Implicit Function Theorem Differentiation Two Dimensional Calculus
Given a function z = f (x, y), we can draw a "topographical map" of f by drawing level curves (or, contour lines) A level curve at z = c is a curve in the x y plane such that for all points ( x , y ) on the curve, f ( x , y ) = cA level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of function when equated to some constant values,example a function of two variables say x and y,then level curve is the curve of points (x,y),where function have constant value 19K viewsLevel curves don't match after rotation of function Consider the general 2D Gaussian function, centered at (05,05), where the covariance matrix can be written in terms of the coefficients a,b, and c as However, given a=125, b=0 and c=,



Problem On Gradient Directional Derivative And Level Curves Leading Lesson




How Do You Sketch Level Curves Of Multivariable Functions Krista King Math Online Math Tutor
The graph itself is drawn in an ( x, y, z) coordinate system Remark 2 Level curves of the same function with different values cannot intersect Remark 3 Level curves of utility functions are called indifference curvesAbstract If H is an arbitrary harmonic function defined on an open set Ω⊂ℂ, then the curvature of the level curves of H can be strictly maximal or strictly minimal at a point of Ω However, if Ω is a doubly connected domain bounded by analytic convex Jordan curves, and if H is harmonic measure of Ω with respect to the outer boundary ofA level curve of a function f (x, y) is the curve of points (x, y) where f (x, y) is some constant value A level curve is simply a cross section of the graph of z = f (x, y) taken at a constant value, say z = c A function has many level curves, as one obtains a different level curve for each value of c in the range of f (x, y)




Level Curves And Implicit Differentiation Studocu




Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id
Are level curves of harmonic functions We may immediately rule out ellipses, for a harmonic function which vanishes on a closed curve must vanish identically Of course, if we permit the function to have singularities this is no longer the case, eg the harmonic function log r vanishes on the unit circle, and has only one finite singularityLevel Curves and Contour Plots Level curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constantFind stepbystep solutions and your answer to the following textbook question Describe the level curves of the function Sketch a contour map of the surface using



1




Describe The Level Curves Of The Function Z 8 2x 7y Chegg Com
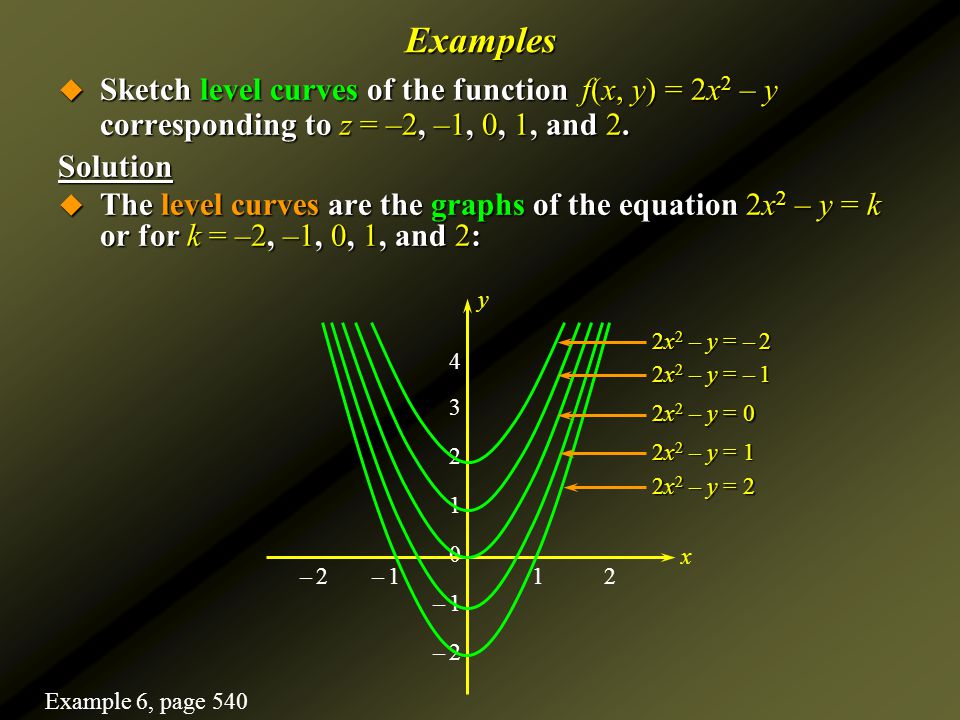
Where f(x;y)=x3 y3 −3xyConsequently,Equation 6 is the level curve f(x;y) = 0 of the function f(x;y)=x3y3−3xy You can plot a single level curve of a function by using Matlab's contourcommand in the form contour(x,y,z,c c) The following commands should produce an image similar to that in Figure 7 Note how a ner meshSketch the level curves of the function corresponding to each value of z f(x, y)=\sqrt{16x^{2}y^{2}} ;Given a functionf(x, y), the setf(x, y) =c= const is called acontour curveorlevel curve off For example, forf(x, y) = 4x2 3y2the level curvesf=care ellipses ifc >0 Level curves allow to visualize functions of two variablesf(x, y) ExampleForf(x, y) =x2−y2



Www Math Uci Edu Remote Teaching Lecture Notes Of Hamed Math 2d lecture notes Lecture note 14 1 Pdf



Http Www Personal Psu Edu Sxj937 Math111 Lecture 11 Pdf
Functions This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both andLevel curves The two main ways to visualize functions of two variables is via graphs and level curves Both were introduced in an earlier learning module Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = c Notice the critical difference between a level curve CLevel Curves We are given a function two variables {eq}f(x,y) {/eq} The level curves are represent the set of points in the xy plane where the function assumes a constant value



8 Calculus Of Several Variables Functions Of Several Variables Ppt Download



Vb Helper Howto Draw Contour Plots Level Curves For A Function With Known Derivatives
Homework Statement I have this function of two variables f(x,y)=x^24xy^2 Where I have to compute the level curves for f(x,y)=3, 2, 1, 0, 1 Homework Equations The Attempt at a Solution So yeah well I know that I have to draw the following curves Level curves of function at z=0 Consider the function f ( x, y) = ( x − 1) 2 y e x 3 y Setting it equal to zero, we get x = 1 or y = 0 According to my understanding, these two lines should be the level curves The whole point of a "level" curve is that the function stays at the same "level", ie the same value The level curve is f(x,y)= yx 2 y 2 = 3 Yes, your tangent line is correct




Gate Ese Level Curves And Surface Of A Function In Hindi Offered By Unacademy
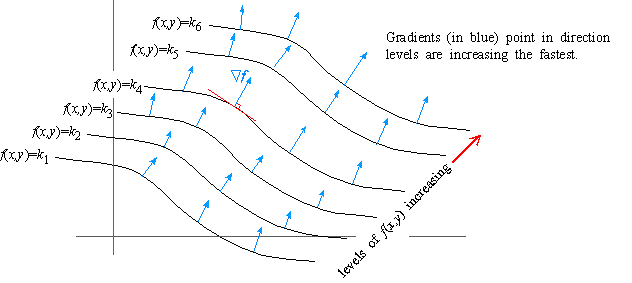



Gradients And Level Curves
So, a topographic map, this one from the US geological survey shows you, basically, all the level curves of an altitude function on a piece of land So, you know that if you walk right along these curves, you will stay along the same height And you know that if you walk towards, these don't have numbers Let me find a place with numbers A level curve of a function f(x,y) is a set of points (x,y) in the plane such that f(x,y)=c for a fixed value c Example 5 The level curves of f(x,y) = x 2 y 2 are curves of the form x 2 y 2 =c for different choices of c These are circles of radius




The Field Of The Condenser And The Level Curves Of The Function U For Download Scientific Diagram




Draw The Level Curve Of The Function F X Y X Y Containing The Point 3 3 Study Com




Level Sets Math Insight




Note On The Curvature Of Orthogonal Trajectories Of Level Curves Of Green S Function Pnas




13 1 Functions Of Several Variables Mathematics Libretexts




Lecture Notes Chapter 1 1 Part2 Contourlines Level Curves And 3d Graphs Pdf
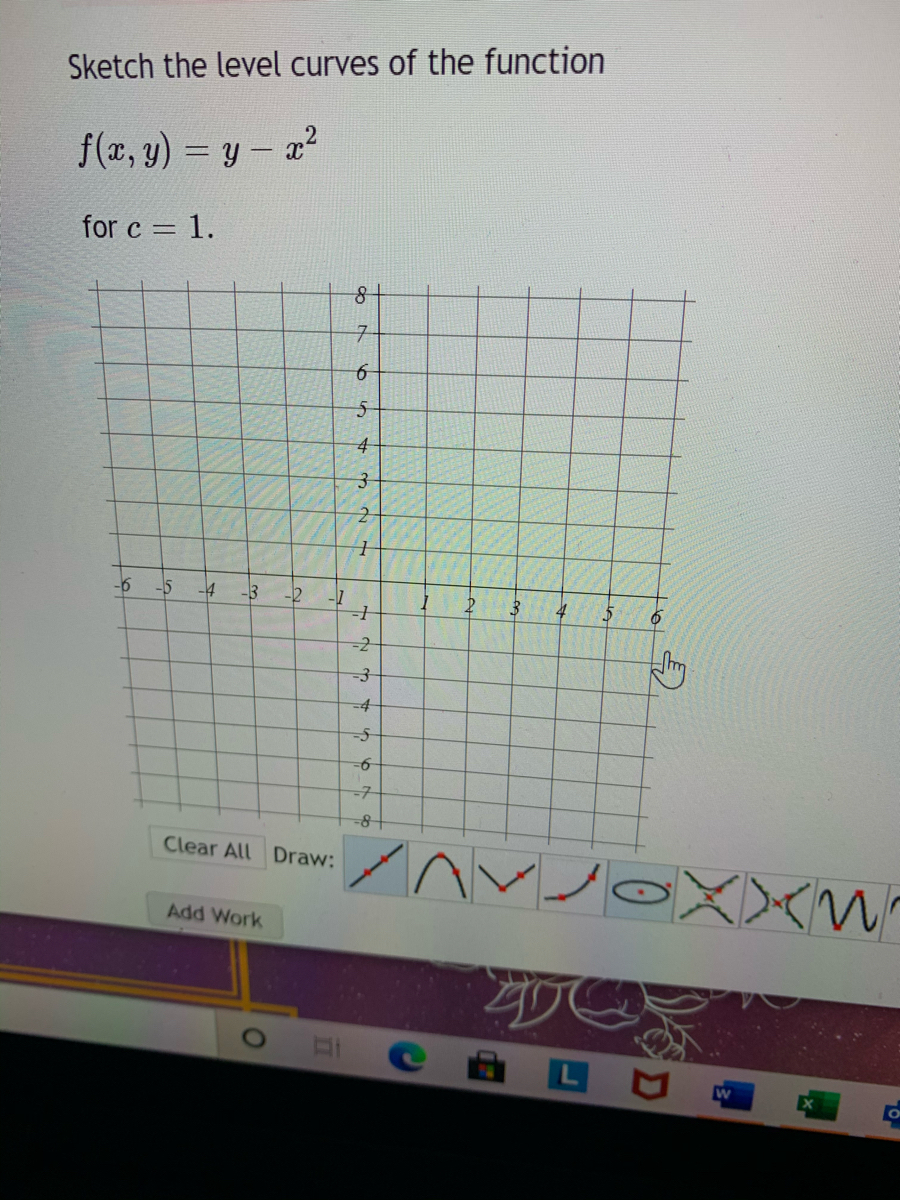



Answered Sketch The Level Curves Of The Function Bartleby




Draw A Contour Map Of The Function Showing Several Level Curves F X Y Y 8x 2 Brainly Com
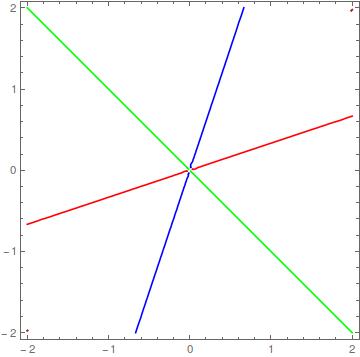



Find Two Level Curves Of The Function F X Y X Y X Y X Y And Sketch Them Socratic




Get Answer Figure 18 61 Shows Level Curves Of The Function F X Y A Transtutors




Lesson 15 Gradients And Level Curves




Sketch The Level Curves Of The Function F X Y X Y 4 Mathematics Stack Exchange




Finding A Function With Level Curves Mathematics Stack Exchange




5 These Are The Level Curves Of A Smoothly Varying Function F X Y 4 A At Homeworklib




Level Curves Of The Error Function Download Scientific Diagram
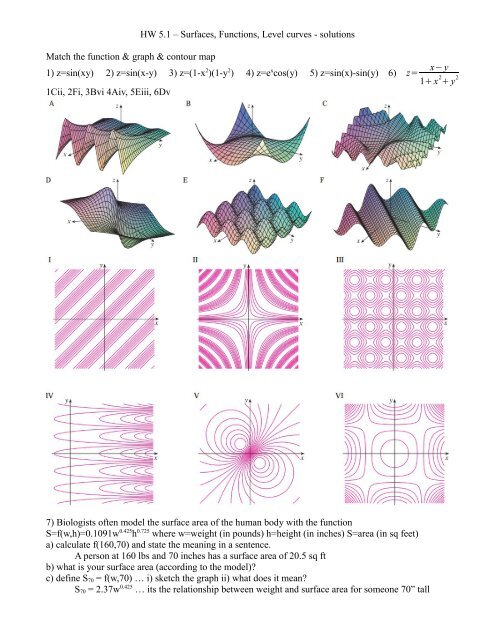



Hw 5 1 A Surfaces Functions Level Curves Solutions Match The



Www Jstor Org Stable



Www Jstor Org Stable




Level Sets Math Insight




1 Sketch A Few Of The Level Curves Of The Function F X Y Surface Z Homeworklib
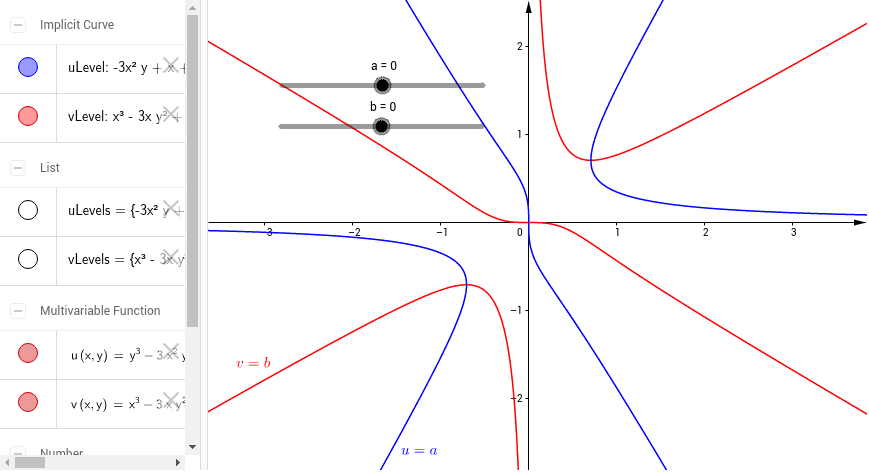



Level Curves Geogebra




Level Curves




How To Sketch Level Curves Youtube




Level Sets Ximera



Calculus Iii Functions Of Several Variables




Level Curves
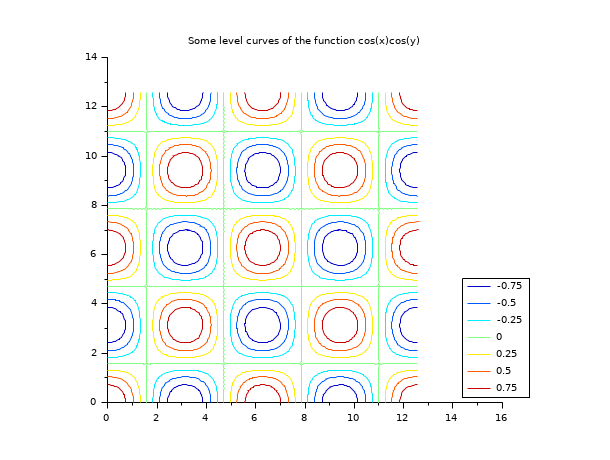



Contour2d Level Curves Of A Surface On A 2d Plot
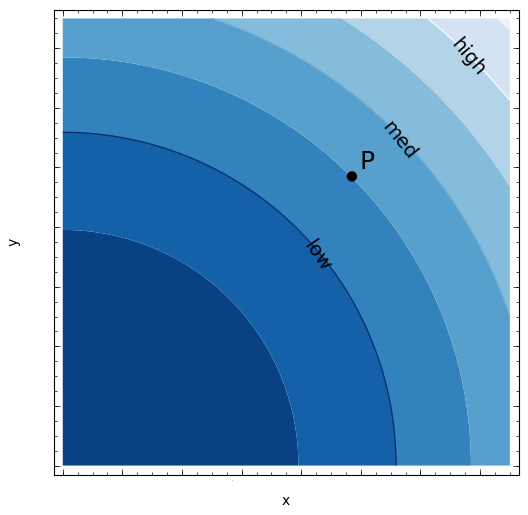



Hgm4 14 Review 71 Gradients Etc Pg Query



Multivariable Functions Level Curves And Partial Derivatives




Graphs And Level Curves




Level Curves



How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 1 Youtube




Make A Contour Plot Showing At Least 3 Level Curves For The Function H X Y Ln X 2 Frac Y 2 4 Study Com



1




Level Curves




Calculus Iii Functions Of Several Variables




Solved Example 11 Sketch The Level Curves Of The Function Chegg Com



Function Range And Level Curves Math 2224 Docsity



Level Curves Geogebra




Calculus 11 1 Functions Of Several Variables Flashcards Quizlet




Contour Maps In Matlab



Sketching Surfaces In 3d



Describe The Level Curves Of The Function Z X2 Chegg Com




Level Curves Of Functions Of Two Variables Youtube




Level Set Examples Math Insight




Lesson 15 Gradients And Level Curves



Solved The Figure Shows Level Curves Of A Functio




E Ana The Gradient Iv 1 The Level Curves Of The Function Z Fix Y Are Sketched In The Figure Bel Homeworklib



Solved Sketch Several Level Curves Of The Function F X Y E X Y




Level Set Wikipedia




Level Curves For The Riemann Zeta Function Maths Paper Graphic Zeta




The Level Curves Of The Function U For The Condenser In Example 6 3 For Download Scientific Diagram




Calculus 11 1 Functions Of Several Variables Flashcards Quizlet



Www Usna Edu Users Math Uhan Sm223 Lessons 12 level curves Pdf



1




Calculus Iii Functions Of Several Variables



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework13 1 Ans Pdf



Level Sets Ximera
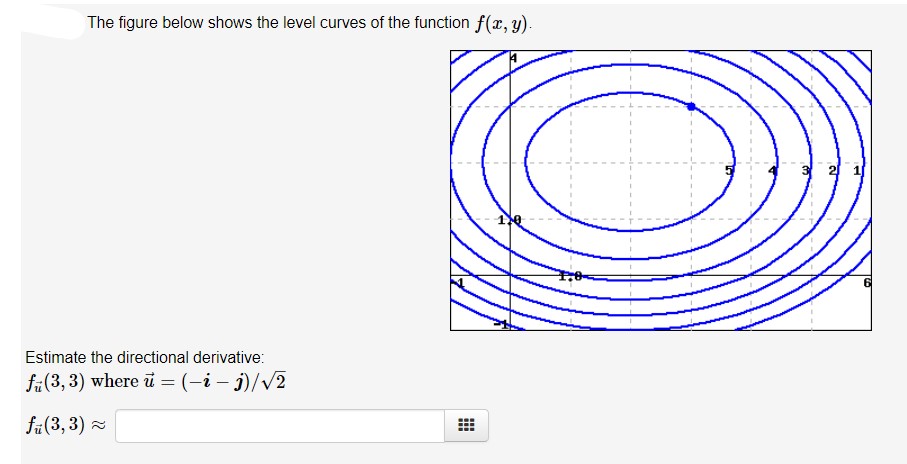



Answered The Figure Below Shows The Level Curves Bartleby



Draw Level Curves For Functions Of Two Variables In C C Helper



0 3 Visualizing Functions Of Several Variables



Relief Functions And Level Curves
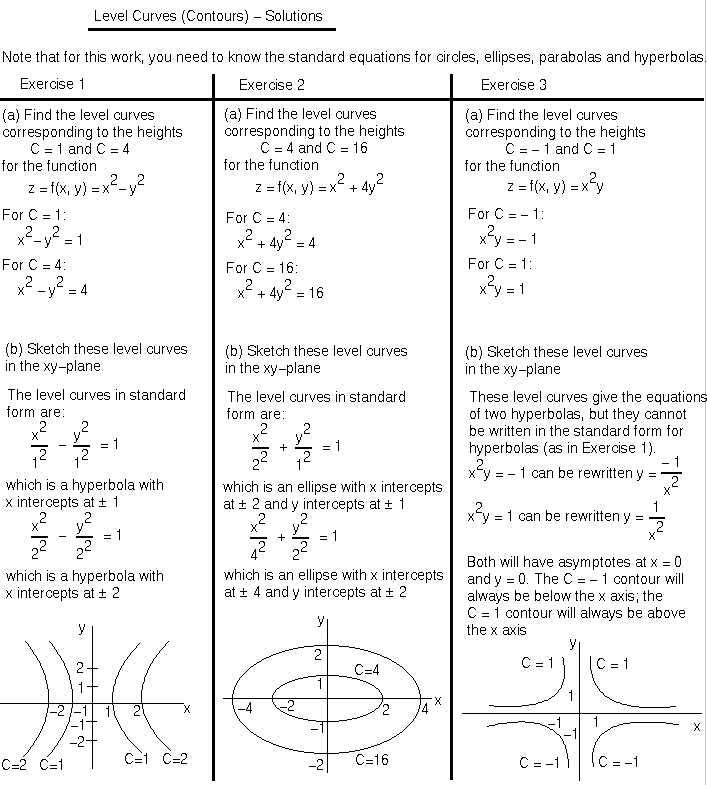



Functions Of Two Variables Math100 Revision Exercises Resources Mathematics And Statistics University Of Canterbury New Zealand




Use The Level Curves Of The Function To Determine If Each Partial Derivative At The Point P Is Positive Negative Or Zero Mathematics Stack Exchange



Level Curves




Describe The Level Curves Of The Function Z X2 Chegg Com



0 3 Visualizing Functions Of Several Variables



1




Matlab How Can I Get The Expression Of The Level Curves Of A Function Stack Overflow



Users Math Msu Edu Users Bellro Lb2sp13 S4 Pdf




Graphs And Level Curves




Help With Partial Derivatives On A Level Curve Calculus




Univ Vector Calculus Drawing A Contour Map With Level Curves Learnmath
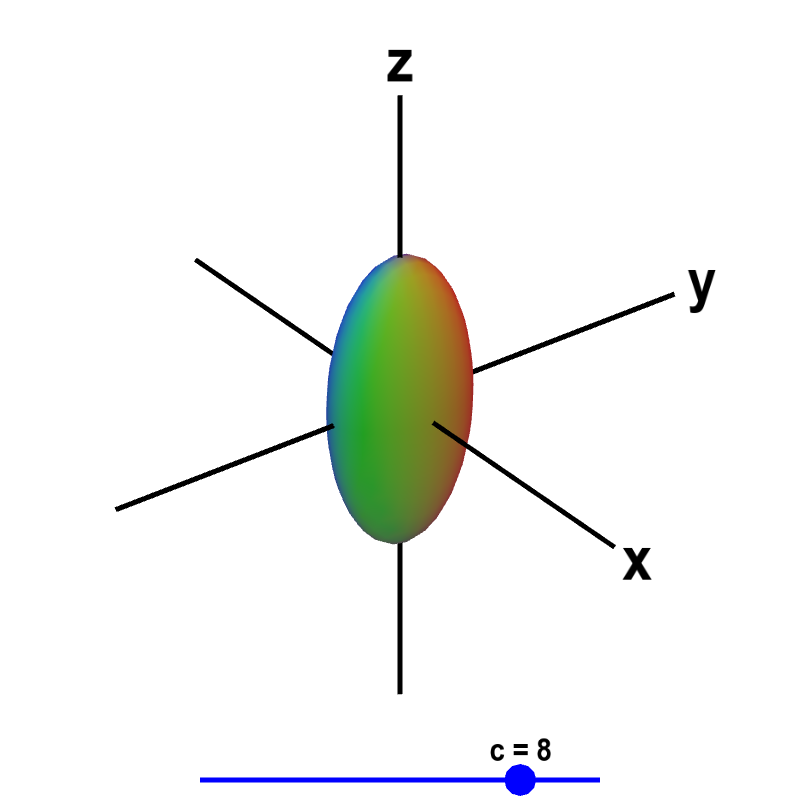



Level Sets Math Insight



Www3 Nd Edu Taylor Math550 Images Currentexamsolutions Exam2f16 Pdf




Level Set Wikipedia



Http People Math Harvard Edu Knill Teaching Summer16 Handouts Week2 Pdf




Sketch The Level Curves Of The Function G X Y Chegg Com



Www Math Uci Edu Remote Teaching Lecture Notes Of Hamed Math 2d lecture notes Lecture note 14 1 Pdf




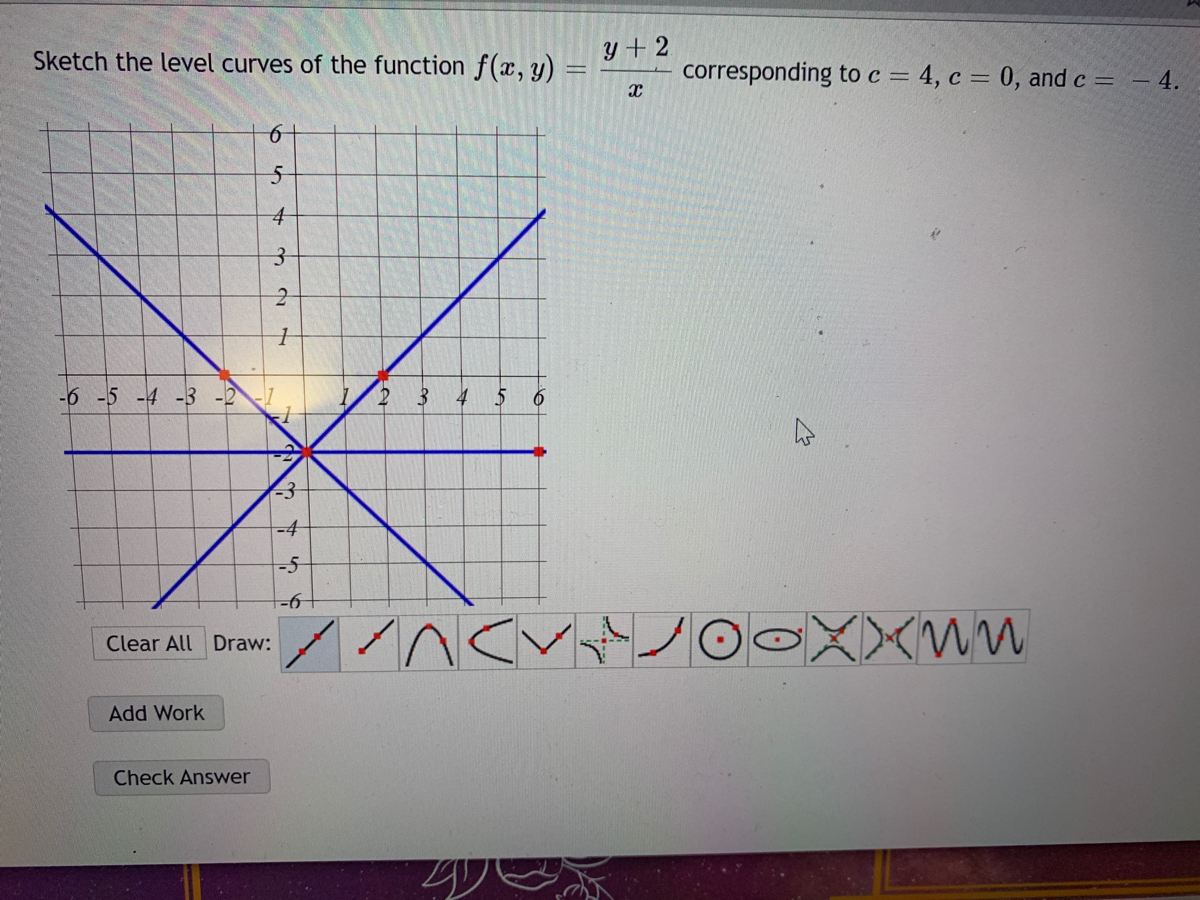
7 Sketch The Level Curves Of The Function Correspo Gauthmath



0 件のコメント:
コメントを投稿